© Profe Mobius
Indice
Introducción
Lección 1: La Division
Lección 2: División con dos dígitos
Lección 3: División con tres dígitos
Lección 4: Divisor de dos dígitos
Lección 5: Ladivision entre múltiplos de diez
Introducción
Sabemos que la división es un poco difícil de entender y algunas personas no quieren saber nada sobre este asunto. Pero la verdad es que, si sigues el método que te presnetamos, puedes aprender de volada.
Advertencia: Para aprender a dividir es necesario saber la tablas de multiplicar, pues la división es como la multiplicación pero al revés. Si necesitas repasar tus tablas, te sugiero acudas a este sitio en español:
https://www.tablasdemultiplicar.com/
Veamos un ejemplo bien sencillo. En las manos tenemos 10 dedos y si los repartimos o dividimos entre las dos manos, resulta que tenemos 5 dedos en cada mano. Decimos que 10 entre 2 es igual a 5, es decir, que el 2 cabe 5 veces en el 10
También podemos ver que 10 entre 5 = 2, es decir, que el 5 cabe dos veces en el 10. Esto quiere decir que si repartimos los 10 dedos de 5 en 5, necesitamos únicamente dos manos.
Podemos ver la relación entre la división y la multiplicación como sigue:
División 10 ÷ 2 = 5 10 ÷ 5 = 2
Multiplicación 10 = 5 x 2 10 = 2 x 5

La División
En la división hay tres términos que debes aprender:
Dividendo es la cantidad que vamos a dividir
Divisores la cantidad entre la que se va a dividir
Resultado es el cociente de dividendo÷ divisor
Remanente que explicaremos más adelante
En la operación 20 ÷ 4 = 5
el dividendo es
20
el divisor es 4
el resultado es 5
Podemos verlo de esta manera:
5 es el número de veces que el número 4 cabe en el 20
5 + 5 + 5 + 5 = 20
Toma un puño de monedas de 5 centavos y colócalas en una mesa. ¿Cuántas necesitas para tener 20 centavos? La respuesta es 4 obviamente.
Pregunta ¿Cuántas monedas de 5 centavos necesitas para tener un quarter de 25 centavos?

Remanente
Este es un concepto que parece complicado pero no lo es. Le pregunté a mi nieta de 5 años cómo le haría para repartir 5 paletas entre sus dos hermanos. Usando sus manitas, en una mostraba 3 deditos y en la otra 2 y me dijo: “le doy dos 2 paletas a cada uno y me quedo con la que sobra”. Esto es lógica infantil: reparto parejo y el remanente me lo quedo.
División con dos dígitos
Supongamos que tienes 14 barras de chocolate y las quieres dividir entre tus 3 amigos de tal manera que cada uno reciba la misma cantidad de chocolate. Hay dos maneras de solucionar el problema. La siguiente figura te va a ayudar a entender como dividir las barras entre los tres amigos/
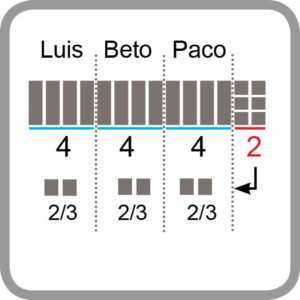
Primera
Como la división es la multiplicación al revés, podemos preguntar ¿Qué número multiplicado por 3 se acerca a 14? Obviamente es el 4 pues 4 x 3 = 12 con un remanente de 2 barras. Le doy 4 barras a cada uno y tengo que repartir las otras dos. Entonces parto cada una de esta barras en 3 partes iguales de tal manera que me quedan 6 pedacitos de chocolate del mismo tamaño de tal manera que a cada uno le tocan 2 pedazos. Al final cada uno tendrá 4 barras más 2 terceras partes de barra.
Segunda
Usar el procedimiento de la división (long division) para que puedas resover cualquier problema. Todo está en utilizar lo que vimos en el párrafo anterior y colocar el dividendo y el divisorcomo se muestra:
![]()
En la primera parte de este ejemplo vimos que el primer dígito del resultado es 4, así que lo anotamos en el espacio del resultadoy lo multiplicamos por el divisorque son tus 3 amigos de tal manera que 4 x 3 =12. Coloca esta cantidad abajo del dividendocon signo negativo. Haz la resta y obtienes el remanenteque es 2 como se indica:
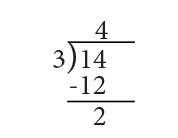
Esta operación indica que 14 dividido entre 3 resulta en 4 con un remanente de 2.
Lo comprbamos: 4 x 3 + 2 = 12+2 =1 4
Puedes dar 4 barras a cada uno de tus amigos pero te faltaría repartirles las 2 del remenente. Continuemos con la división. Como ya no hay más dígitos (números) a la derecha del dividendo 14, añades un punto decimal en el resultado para que en vez de 4 se lea 4. (se lee cuatro punto) y le añades un cero al remanente 2 para que sea 20. Ahora tenemos que calcular que número multimplicado por 3 se acerca a 20.
Veamos que pasa si escogemos uno de estos números: 5, 6 y 7:
5 x 3 = 15
6 x 3 = 18
7 x 3 = 21
Como puedes ver, el 5 se queda corto y el 7 se pasa del 20, así que debemos escoger el 6.
Multiplica este número por el divisor y lo colocas abajo del 20 con signo negativo como se indica en la siguiente figura. Haz la resta y obtienes el nuevo remanente 2.
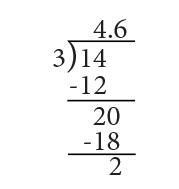
Hasta aquí la división indica que puedes dar 4.6 barras a cada uno de tus amigos. Para obtener más exactitud debes colocar otro cero en el remanentey continuar con la división tal como se hizo en el paso anterior. Obtendrás el resultado final de 4.66
Comprobación:
4.66 x 3 = 13.98. En tu calculadora haz la división 14 ÷ 3 y verás el resultado como 4.66666667 que puedes expresar como 4.67 x 3 = 14.01 En la mayoría de las veces dos decimales son suficientes en una división.
Al principio de esta sección vimos que cada uno de tus amigos recibiría 4 + 1/3 + 1/3 barras de chocolate que es exactamente 4 barras y 2/3 de barra = 4.67
Por ambos caminos llegamos a la misma solución, sólo que repartir 4.67 barras de chocolate es más difícil de visualizar que repartir 4 barras más 2/3 a cada persona.

División con tres o más dígitos
Dividir 2580 entre 5.
![]()
El primer dígito de 2580 es el 2 pero es menor que el divisor, así que debemos tomar los dos primeros dígitos que forman 25. El divisor cabe 5 veces en el número 25 así que lo colocamos en la respuesta. El producto de 5 x 5 lo colocamos como negativo y hacemos la resta que da 0.
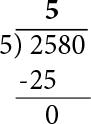
En este caso el remanente es cero. Bajamos el siguiente dígito del dividendo, que en este caso es el 8 y lo colocamos en el remanente al lado del cero como indica la flecha de la figura. Continuamos con la división y vemos que el 5 cabe 1 vez en el 8. Colocamos el 1 en la respuesta y lo multiplicamos por el divisor. El producto de 1 x 5 lo colocamos en negativo abajo del ocho y hacemos la resta que nos da el nuevo remenente que es 3.
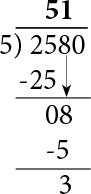
Ahora bajamos el último dígito del dividendo que es 0 y obtenemos el nuevo remanente 30. La multiplicamos el 6 por el divisor nos dfa 30 que colocamos como negativo y hacemos la resta que nos da 0. Como ya no hay más dígitos en el dividendo, hemos terminado la división. La solución es 516 con cero de remanente.
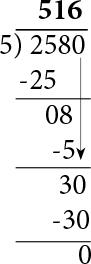

Divisor de Dos Dígitos
Cuando el divisor contiene dos o más dígitos, la división opera de la misma manera que hemos visto, pero como no memorizamos las tablas de multiplicar de dos dígitos, tenemos que proceder a prueba y error. Veamos este ejemplo:
![]()
Los primeros dos dígitos del dividendo que forman en número 10 son menores que el divisor y por lo tanto tenemos que irnos al “tercer” dígito que forma el número 105. Tenemos que pensar por cúanto tenemos que multiplicar el divisor para que se acerque a 105 sin que sea mayor que ese número. La siguiente tabla es lo que se llama calcular a prueba y error:
10 x 13 = 130 resulta mayor y no nos sirve
9 x 13 = 117 resulta un poco mayor y tampoco sirve
8 x 13 = 104 resulta ser el número adecuado
Colocamos el 8 sobre el 5 del dividendo para indicarnos que en el primer paso estamos dividiendo 105 ÷ 13.
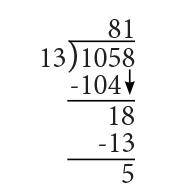
Ya podemos continuar con el proceso de la división que conocemos:
1) Multiplicamos 8 x 13 = 104 que colocamos con signo negativo abajo del número 105
2) Obtenemos un remanente de 1
3) Bajamos el 8 para poder dividir 18 entre 13
4) El 13 cabe una vez en el 18, así que colocamos un 1 en el resultado
5) Multiplicamos 1 x 13 = 13 y lo colocamos debajo del 18 con signo negativo
6) Hacemos la operación 18 – 13 = 5
7) Vemos que 1058 ÷ 13 = 81 con un remanente de 5

La División entre múltiplos se diez
La división entre múltiplos de diez: 10, 100, 1000 etc es muy fácil pues solamente tienes que quitar al dividendo la cantidad de ceros del divisor. Vamos a dividir $10,000 entre distintos grupos de personas
10,000 ÷ 10 = 1,000
le quitamos un cero a 10,000
10,000 ÷ 100 = 100
le quitamos dos ceros a 10,000
10,000 ÷ 1,000 = 10
le quitamos tres ceros a 10,000
10,000 ÷ 10,000 = 1
le quitamos cuatro ceros a 10,000
La división con Uno y Cero
Recuerda estos tres casos:
10 ÷ 1 = 10 la división entre 1 es el mismo numero
0 ÷ 1 = 0 el cero nunca se puede dividir entre otro número
1 ÷ 0 = ? ningún número se puede dividir entre cero
Que es el Infinito
Cuando divides un número entre cero, el resultado es infinito. Si lo quieres comprobar puedes usar tu calculadora. Divide cualquier número, el que tu quieras, entre cero. Te marcará “Error” porque el resultado es infinito.
Si tienes preguntas o comentarios,
envíame un email a
profe.mobius@pactmovil.org

