© Profe Mobius

El perímetro es el contorno de una superficie plana, es decir, la medida de todos sus lados ya sean rectos o curvos. El cálculo del perímetro se utiliza en la industria de la construcción, agricultura, arquitectura, jardinería, panadería, costura y decoración para nombrar sólo unas.

Figuras geométricas rectas

Para las figuras que tengan todos sus lados iguales, por ejemplo de 2 metros, el perímetro será:
Para un cuadrado:
2 + 2 + 2 + 2 = 8    2 x 4 = 8

Para un triángulo:
2 + 2 + 2 = 6 m     2 x 3 = 6

El rectángulo tiene dos lados cortos del mismo tamaño y dos lados largos iguales. Si los lados cortos miden 3 m y los largos 6 m:
Perímetro = 2 x 3 m + 2 x 6 m = 6 m + 12 m = 18 m

Ejemplo 1
Tenemos un terreno rectangular que mide 10 m de ancho por 20 m de largo. Queremos colocar postes de madera a cada 2 metros alrededor del terreno. ¿Cúántos postes tenemos que comprar?

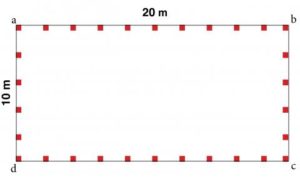
El perímetro es = 20 + 10 + 20 + 10 = 60 m
La cantidad de postes = 60 ÷ 2 = 30 postes

Ejemplo 2
Una costurera tiene que hacer 100 banderas con 3 rectángulos del mismo tamaño en tres colores distintos y un contorno de oro como se muestra en la figura:

¿Cuántos metros de paño de 20cm de ancho debe comprar para cada color, y cuántos metros de hilo dorado para el contorno?

Todos los rectángulos tienen 30 cm de alto y 20 cm ancho que es la medida del paño. Por lo tanto, sólo debemos multiplicar los 30 cm de alto de la bandera por la cantidad de banderas como sigue:
Paño de 20 cm de ancho para cualquier color = 30 cm x 100 banderas =  3000 cm = 30 metros

El hilo dorado solamente se utiliza para el perímetro exterior de la bandera. Por lo tanto la cantidad de hilo dorado es:
Para 1 bandera = 2 x 30 cm + 6 x 20 cm = 180 cm = 1.80 m
Para 100 banderas = 100 x 1.80 m = 180 m

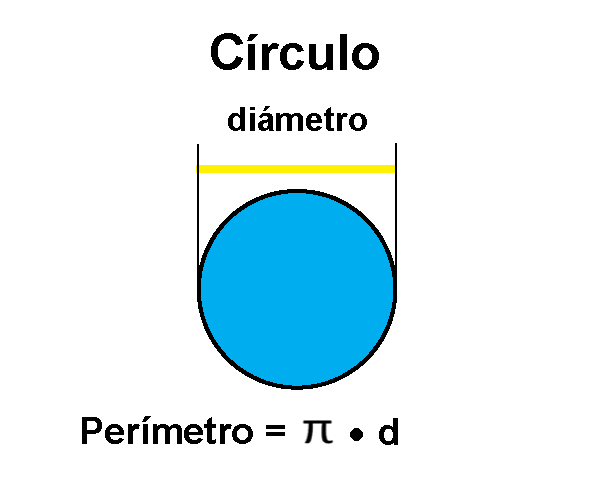
Círculo
En cualquier círculo su diámetro cabe 3.14 veces en su circunferencia. Esta medida se conoce como Pi y se utiliza el símbolo π.
Entonces  π = 3.14
(Nota: para evitar confusiones, la multiplicación la señlaremos con un punto en lugar de una x).

El perímetro de un cíuculo es Pi por su diámetro =  π • d

Ejemplo 3
Si las llantas de un carro miden 22 pulgadas de diámetro, ¿cuánto avanza el carro cada vez que las llantas dan una vuelta completa?
La circunferencia (perímetro) de cada llanta es de:
22 • π = 22 • 3.14 = 69 pulgadas.
Entonces, por cada vuelta completa de la llanta el carro avanza 69 pulgadas.

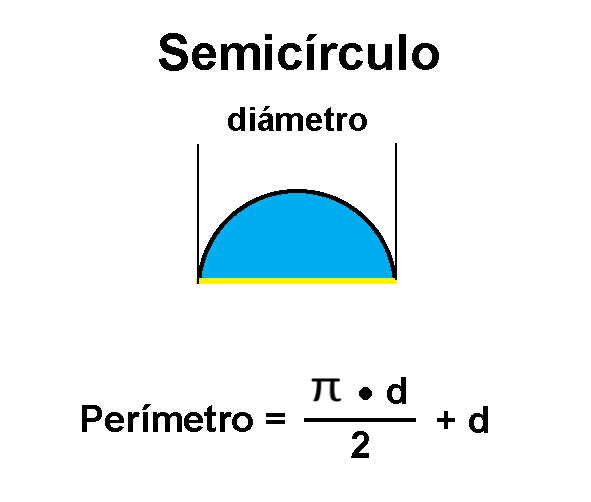
Semicírculo y otras secciones del círculo
El semicírculo es exactamente la mitad de un círculo. Para calcular su perímetro tenemos que hacer dos cálculos:
1) Calcular el perímetro del círculo completo y dividirlo a la mitad para que tengamos el perímetro del arco (la parte curva del semicírculo).
2) Añadir la parte recta del semicírculo que es exactamente su diámetro.

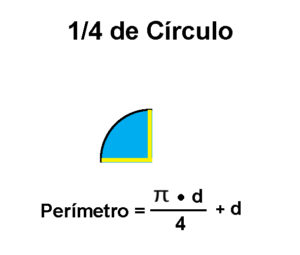
Para calcular el perímetro de una figura que sea 1/4 de círculo tenemos que hacer dos cálculos:
1) Calcular el perímetro del círculo completo y dividirlo entre 4 para que tengamos el perímetro del arco.
2) Añadir la parte recta del semicírculo que es exactamente su diámetro de las dos figuras anteriores.

Ejemplo 4
Supongamos que el diámetro del círculo es de 5 ft. ¿Cuáles son los perímetros del semicírculo y de 1/4 de círculo (un pedazo de pizza)?

Semicírculo
El perímetro para el círculo es 5 • π  = 15.7 ft
El perímetro del arco del semicírculo es 15.7 ÷ 2 = 7.85 ft
La parte recta del semicirculo (diámetro) = 5 ft
El perímetro del semicírculo es: 7.85 + 5 = 12.85 ft

Un cuarto de círculo
Para calcular el perímetro de ¼ de círculo:
Perímetro del arco = 15.7 ÷ 4 = 3.92 ft
Perímetro de las partes rectas = 5 ft
Perímetro de ¼ de círculo = 3.92 + 5 = 8.92 ft

¿Tienes preguntas o comentarios?
Envíame un email a
profe.mobius@pactmovil.org