© Profe Mobius
El tema de las coordenadas cartesianas es fundamental en matemáticas, sobre todo en geometría analítica y cálculo. No vamos a presentar las aplicaciones, sino nada más una introducción para saber son.
Se denominan coordenadas cartesianas en honor a René Descartes (1596-1650), el célebre filósofo y matemático francés creador de la geometría analítica. Descartes tuvo la idea de crear un sistema de coordenadas en las que pudiera representar las ecuaciones de las figuras geométricas y así poder calcular con precisión la posición exacta de un punto, sobre todo cuando el objeto está en movimiento. Tuvieron que pasar siglos para que Newton y Leibnitz inventaran el cálculo y se pudieran resolver estos problemas utilizando las coordenadas cartesianas.
Sin las ecuaciones no podemos determinar exactamente en donde está un tracto-camión que va de Houston a Dallas a 55 millas por hora. Solamente cuando usamos la ecuación v = d ÷ t podemos calcular que la distancia es d = v × t así que lo único que tenemos que hacer es ver el reloj para saber hace cuanto tiempo salió de Houston localizar al tracto-camión. Si lleva dos horas de viaje entonces está a 55 × 2 = 110 millas de Houston.
Gráficas en Matemáticas
Los siguientes ejemplos representan figuras geométricas a base de ecuaciones.
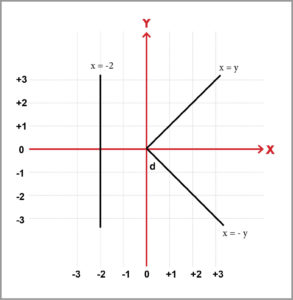
Líneas rectas:
La línea vertical se describe solamente con su posición al eje Y. En esta figura la recta vertical es x = – 2. Si estuviera a la derecha del eje Y la ecuación sería x = 2. Una recta horizontal arriba del eje X sería y = 2; si estuviera abajo del eje X sería y= -2.
Curvas:
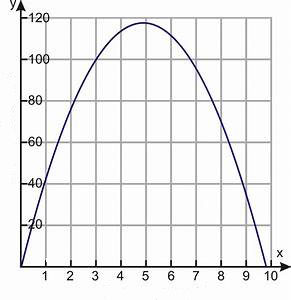
Ahora veamos la gráfica de una parábola con la ecuación y = x ²
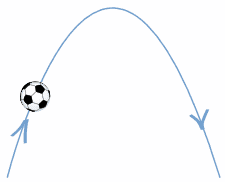
En la gráfica de abajo el eje X representa el tiempo contado en unidades de tiempo que en este caso son segundos. El eje Y representa unidades de altura (metros, pies, cm, etc). La curva la podemos ve en cualquier fuente de agua, también cuando usamos una manguera para regar a flores y, por supuesto, cuando el portero hace un saque de meta.
Estructura de las Coordenadas Cartesianas
Las coordenadas cartesianas contienen dos ejes perpendiculares: “X” horizontal y “Y” vertical que se cruzan en lo que se llama el origen, representado en la figura siguiente por la letra “a”, aunque es común que no aparezca marcada.
A la derecha y a la izquierda sobre el eje X dibuja líneas a igual distancia de 1 cm y lo mismo haces con el eje Y dibujando rayas hacia arriba y hacia abajo a las mismas distancias de 1 cm. De esta manera obtenemos una cuadrícula en la que cada cuadro mide 1 cm por lado.
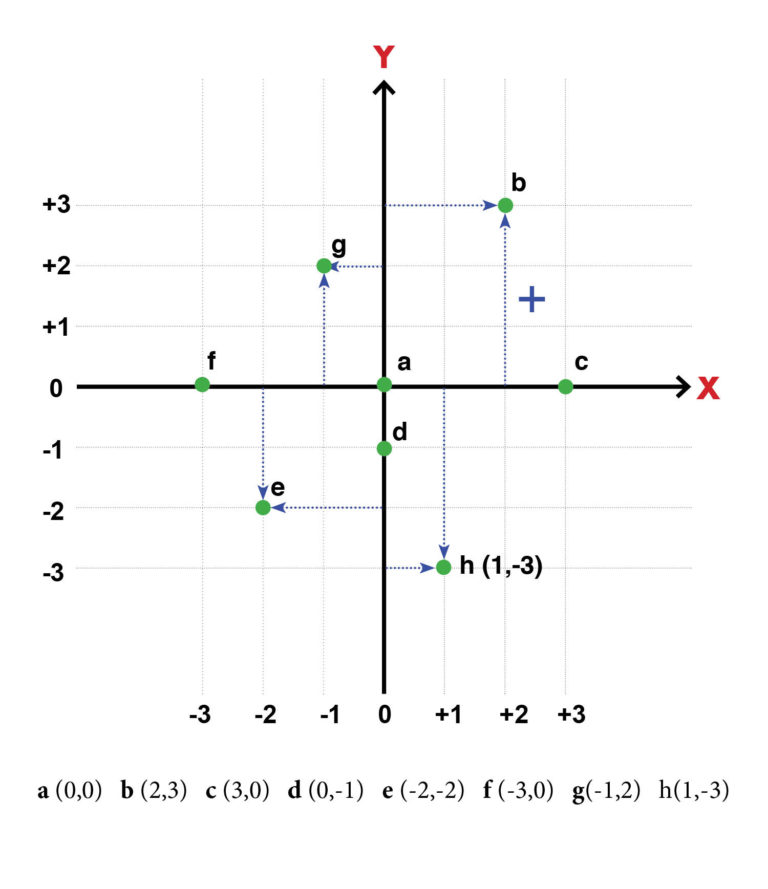
En la figura hemos colocado ocho puntos verdes que pueden representar cualquier cosa como las ventas del mes, consumo de gasolina, tráfico a una tienda o lo que se esté midiendo.
Para indicar su posición, o sea su valor, que puede ser de dólares, galones de gasolina o número de personas, simplemente medimos la distancia del punto a cada uno de los ejes que pueden ser:
(+) positivos si se localizan arriba del eje X o a la derecha del eje Y
(–) negativos si se localizan abajo del eje X o a la izquierda del eje Y
Para entender bien cuáles valores son positivos y cuáles negativos, hemos colocado flechas en la figura. Los puntos tienen valor positivo si la punta de la flecha va hacia la derecha o hacia arria, y son negativas si las puntas van para abajo o hacia la izquierda. No necesitas usar estas flechas en tus gráficas, las usamos aquí para explicar el signo de los números.
De esta manera el punto “h” se encuentra en x = 1 con y = –3 y se escribe: h (1,–3).
Podemos localizar cada punto señalándolo con un paréntesis con dos valores separados por una coma. Adentro del paréntesis escribimos primero el valor de X y luego el de Y. En la parte inferior de la gráfica aparecen los valores de todos los puntos.
Podemos dividir cada centímetro de la cuadrícula en 10 partes cuando necesitamos obtener valores con más precisión. Por ejemplo, la cruz azul esta localizada en (2.5 , 1.5).
¿Tienes preguntas o comentarios?
Envíame un email a
profe.mobius@pactmovil.org


