© Profe Mobius
El álgebra es una rama de las matemáticas que emplea números, letras y signos para hacer referencia a las distintas operaciones aritméticas que se realizan. Cualquier persona que sepa cocinar pozole utiliza el álgebra, pues la receta de la tía Cuca es una ecuación en donde los ingredientes varían según la cantidad de gentes invitadas.
El álgebra es muy parecida a la aritmética, en donde aprendemos las operaciones de suma, resta, multiplicación y división. La diferencia es que en álgebra utilizamos letras. Tomemos por ejemplo la operación
1 más 2 es igual a 3.
En álgebra la escribimos. a + b = c
Le podemos dar valores distintos a las letras a, b y c
Si a = 1 b = 2 entonces c = 3
Si a= 3 b = 5 entonces c = 8
Indice
Lección 1: La Ecuación
Lección 2: La Incógnita
Lección 3: Las Variables
Lección 4: Operaciones Comunes
Lección 5: Multiplicación y División
Lección 6: Uso de Paréntesis
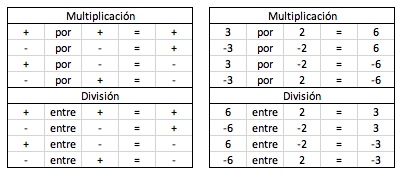
Lección 7: Números Negativos


La Ecuación
Los ejemplos que hemos visto forman lo que en álgebra se conoce como ecuaciones. Expresan cantidades relacionadas entre sí por medio de operaciones de aritmética y el signo de igualdad. Es importante notar que los dos lados de la ecuación deben ser iguales. En la ecuación 1 + 2 = 3 los dos lados son iguales, es decir 3 = 3
En una ecuación podemos pasar cualquier cantidad de uno al otro del signo = pero debemos cambiar su signo. Vamos a ver que sucede con la ecuación si movemos las cantidades.
1 + 2 = 3
Si pasamos el 2 a la derecha tenemos que hacerlo con signo de menos (resta):
1 = 3 – 2 quedando 1 = 1
1 + 2 = 3
Si pasamos el 1 a la derecha lo hacemos con signo de menos, entonces:
2 = 3 – 1 quedando 2 = 2
1 + 2 = 3
Si pasamos la cantidad 3 al lado izquierdo de la ecuación pasa con signo menos:
1 + 2 – 3 = 0
3 – 3 = 0
Es importante notar que en todos los casos los lados de la ecuación son iguales y que obtenemos diferentes resultados según movamos las cantidades de uno a otro lado

La Incógnita
La ecuación 1 + 2 = 3 se escribe en álgebra como sigue:
1 + 2 = x en donde “x” es el valor que queremos encontrar, y como no lo conocemos, decimos que “x” es una incógnita.
Para encontrar el valor de x decimos que resolvemos la ecuación x = 3
Al sustituir el valor de x tenemos 1 + 2 = 3 como ya hemos visto.
Hagamos la siguiente ecuación: 1 + x = 3
Ya vimos que podemos pasar el 1 al lado derecho de la ecuación cambiándole su signo:
x = 3 – 1 cuyo resultado es x = 2
Como vemos, las operaciones en aritmética y álgebra son las mismas.

Las Variables
Ahora vamos a ver operaciones en las que tenemos dos incógnitas que también podemos llamar “variables” pues irán cambiando dependiendo del valor de la otra. En álgebra se usan letras minúsculas para las variables. Veamos el siguiente ejemplo:
a – 4 = b – 2
Si queremos calcular el valor de “a” entonces todas las otras cantidades deben quedar en el lado opuesto de la igualdad:
a = b – 2 + 4
a = b + 2 que es nuestra ecuación “simplificada” es decir, más simple para resolverla.
Como podemos ver, el resultado de la variable “a” depende de la cantidad que le demos a la variable “b”. En álgebra, la variable que no conocemos siempre se pone del lado izquierdo de la ecuación. Más adelante veremos que lo más común es usar la letra “x” como variable. Ahora podemos darle valores a la variable “b” para obtenre los valores de la incógnita “a”:
Para b = 1
a = b + 2 sustituimos el valor de b = 1
a = 1 + 2
a = 3
Para b = 2
a = b + 2 sustituimos el valor de b = 2
a = b + 2
a = 2 + 2
a = 4
Como podemos ver, el valor de la incógnita “a” depende del valor que le demos a la variable “b“.

Operaciones Comunes
En álgebra hacemos operaciones aritméticas con letras. Veamos el caso más sencillo:
x + x = 2 x que es lo mismo que 2x = x + x
2x debe entenderse como 2 por “x”. Para no confundir la variable “x” con el signo de multiplicación, en álgebra se utiliza un punto:
2•x
Si hacemos x= 5 y sustituimos este valor en la ecuación 2x = x + x, tenemos:
2 • 5 = 5 + 5 que resulta 10 = 10
En la misma ecuación 2 x = x + x pasamos una x al lado izquierdo de la ecuación y tendremos que
2 x -x= x
Sustituimos x = 5
2 • 5 – 5 = 5
10 – 5 =5 que resulta 5 = 5
Ejemplo
Supongamos que un dólar es igual a 15 pesos y queremos tener una ecuación que nos permita cambiar pesos por dólares y también dólares por pesos.
Lo primero que debemos hacer es definir los elementos de la ecuación:
“d” es la cantidad de dólares que queremos cambiar a pesos
“p” es la cantidad de pesos vamos a obtener en la operación
15 es el tipo de cambio en pesos por dólar
Entonces si queremos cambiar 4 dólares a pesos:
p = 15 • d = 15 • 4 = 60 pesos

Multiplicación y División
Como ya dijimos, en álgebra la multiplicación no se señala con una “x” porque se puede confundir con la “incógnita x”. Hay dos maneras de señalar una multiplicación:
p = 15 • d se puede utilizar un punto
p= 15 d sin signo que es la manera aceptada
En álgebra, una cantidad que multiplica pasa al otro lado dividiendo, y si está dividiendo pasa multiplicando.
Fíjate como la variable “b” multiplica en un lado y divide en el otro:
a b = c a = c/b c = a b b = c/a
Si queremos saber cuántos dólares son 60 pesos partimos de la ecuación anterior
p = 15 d
Si queremos saber cuántos dólares son $60 pesos, la ecuación queda d = p ÷ 15
Sustituimos el valor de “p” que son los 60 pesos que queremos convertir a dólares:
d = 60 ÷ 15 = 4 dólares

Uso de Paréntesis
En álgebra se pueden agrupar las cantidades usando paréntesis para simplificarlas.
Veamos este ejemplo.
2x + 5x = y
Esta ecuación la simplificamos usando paréntesis, en donde la variable “x” multiplica a la cantidad dentro del paréntesis:
x (2 + 5) = y entonces 7x = y
Ejemplo 2
Vamos suponer que a Rosita y a sus 3 hermanos les gusta desayunar avena con leche. Sin embargo no todos desayunan avena todos los días. Las instrucciones de la caja de avena dicen que para 1 porción (para 1 persona) debemos usar:
Avena: 1 taza
Leche: 2 tazas
Las primera variable que tenemos que considerar es el número de personas que quieren avena cualquier día de la semana. Esta variable puede ser de 1 a 4 personas (Rosita y sus 3 hermanos). Llamemos “p” a esta variable. Hay otras dos variable que son las tazas de leche que llamaremos “m” y las tazas de avena “a”. Podemos ver que la cantidad de tazas de leche es la cantidad de personas multiplicada por 2 y la cantidad de tazas de avena es igual a la cantidad de personas. Entonces
m = p 2 = 2p
a = p 1 = 1p = p
Cuando tengamos en número 1 como multiplicador no lo escribimos. En este caso, la cantidad de avena es igual al número de personas.
Podemos calcular las cantidades de ingredientes para cualquier número de personas que quieran avena:
| “p” | m = 2p tazas | a = p tazas |
| Personas | Leche | Avena |
| 1 | 2 | 1 |
| 2 | 4 | 2 |
| 3 | 6 | 3 |
| 4 | 8 | 4 |